主成分分析是一种常用的多变量统计方法,用于降低数据的维度、探索数据间的关系,并提取数据中的主要信息。本文将以一个具体的例题为例,详解主成分分析的原理和步骤,帮助读者更好地理解和应用这一方法。

标题和
1.引言
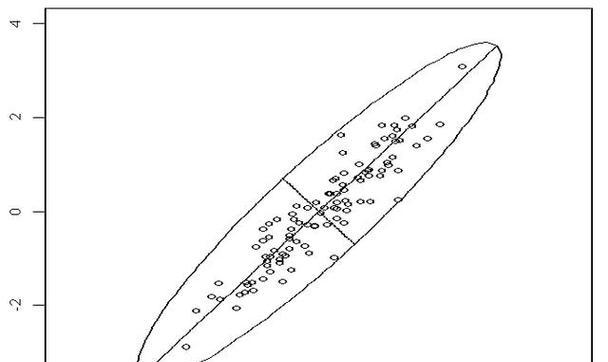
-主成分分析(PrincipalComponentAnalysis,简称PCA)是一种常用的数据降维技术,可以将高维度的数据转化为低维度的特征,保留了数据的大部分信息。
2.例题背景
-假设我们有一份包含多个变量的数据集,我们希望通过主成分分析找到其中最重要的几个变量,并进行维度压缩,以便更好地理解数据集。
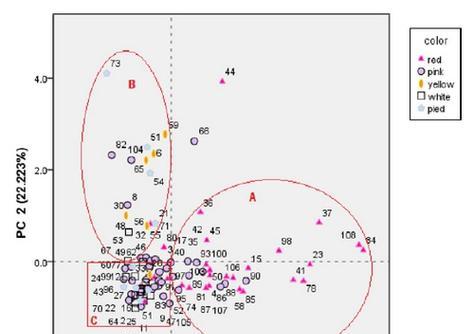
3.数据预处理
-在进行主成分分析之前,需要对数据进行预处理,包括去除缺失值、标准化等。这样可以确保各个变量在同一尺度上进行比较,并减少异常值对结果的影响。
4.计算协方差矩阵
-主成分分析的核心是计算协方差矩阵,它描述了数据中各个变量之间的相关性。通过计算协方差矩阵,我们可以了解哪些变量对数据的解释能力更强。
5.特征值和特征向量
-协方差矩阵的特征值和特征向量是主成分分析的关键,它们代表了数据的方差和变化方向。特征值越大,说明该主成分所包含的信息越多,我们应该保留该主成分。
6.选择主成分数量
-通过观察特征值的大小和累积贡献率,我们可以确定保留多少个主成分。通常,我们选择那些累积贡献率较高的主成分,以保留较多的信息。
7.主成分旋转
-主成分旋转是一种调整主成分方向的方法,旨在使主成分更易解释和解释性。通过旋转后的主成分,我们可以更清晰地理解数据集中不同变量之间的关系。
8.主成分得分
-主成分得分是每个样本在主成分上的投影值,可以用来衡量样本在不同主成分上的表现。通过主成分得分,我们可以识别出数据集中的异常点和群集。
9.主成分分析的应用
-主成分分析在各个领域都有广泛的应用,例如金融风险管理、图像处理、生物信息学等。它可以帮助我们更好地理解数据集,并发现其中潜藏的规律和关联。
10.主成分分析的局限性
-尽管主成分分析有许多优点,但也存在一些局限性。例如,它假设数据集是线性可分的,并且可能无法处理非线性关系。此外,主成分分析结果的解释性也需要谨慎对待。
11.实例讲解
-通过一个具体的例子,我们将展示主成分分析在实际问题中的应用过程。从数据预处理到主成分选择和旋转,帮助读者更好地掌握主成分分析方法的具体步骤。
12.结果解读与讨论
-在完成主成分分析后,我们需要解读和讨论结果。通过解读主成分的特征向量和得分,我们可以获得关于数据集的重要信息,并将其应用于后续的决策和问题解决中。
13.主成分分析与其他方法的比较
-主成分分析与其他降维方法(如因子分析、独立成分分析等)相比,各有优劣。我们将对主成分分析与其他方法进行比较,帮助读者选择适合自己问题的方法。
14.注意事项和应用建议
-在应用主成分分析时,我们需要注意一些常见的问题和陷阱。同时,根据具体问题的特点,我们还可以提出一些应用建议,帮助读者更好地使用主成分分析解决实际问题。
15.
-主成分分析是一种强大的数据分析工具,通过降维和信息提取,可以帮助我们更好地理解数据集和变量之间的关系。掌握主成分分析的原理和应用步骤,将有助于读者在实践中灵活运用该方法。


