在学习过程中,我们经常会遇到需要用分数形式表示数字的情况。掌握打出分数形式的方法不仅可以帮助我们更好地理解和运用知识,还可以提高学习效果。本文将为大家介绍一些有效的方法和技巧,帮助大家在使用分数形式时更加得心应手。

1.分数的概念及表示方法

在开始学习分数之前,我们首先需要了解分数的概念。分数由一个分子和一个分母组成,分子表示被分割物体的部分数量,分母表示总的等份数量。通常用“分子/分母”的形式表示分数。
2.分数的基本运算规则
掌握分数的基本运算规则是使用分数形式的关键。对于加减乘除等基本运算,我们需要根据分数的性质和规则进行相应的运算步骤。
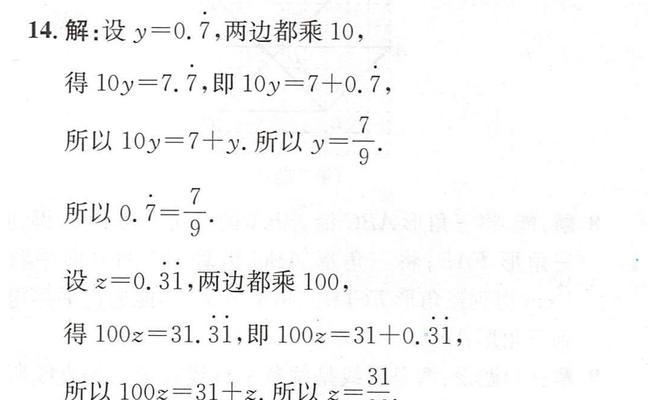
3.转换分数为小数的方法
有时候我们需要将分数转换为小数形式,这样更便于计算和比较。通过将分子除以分母,我们可以得到一个小数值。
4.分数的约分与通分
分数的约分可以将分数化简为最简形式,使得计算更加简便。而通分是将不同分母的分数转换为相同分母的分数,便于比较和运算。
5.带分数的表示与运算
带分数由整数部分和真分数部分组成,可以表示较大的数字。了解带分数的表示方法和运算规则可以帮助我们更好地处理复杂的计算问题。
6.百分数与分数的转换
百分数与分数之间存在一定的转换关系,掌握百分数与分数之间的转换方法,可以方便地进行百分比计算和比较。
7.分数的大小比较
在学习中,我们常常需要比较两个或多个分数的大小。通过将不同的分数转换为相同的分母,我们可以直接比较它们的分子大小来判断大小关系。
8.分数在实际问题中的应用
分数在现实生活中有着广泛的应用。通过学习分数在实际问题中的应用,我们可以更好地理解和运用它们,解决实际问题。
9.分数的乘法与除法应用
掌握分数的乘法和除法应用方法可以帮助我们更好地解决涉及到比例和倍数的问题,如物品的折扣、食谱的调整等。
10.分数的加法与减法应用
分数的加法和减法在实际中也有很多应用场景,如计算时间、长度、体积等。通过学习应用方法,我们可以更好地解决这些实际问题。
11.利用分数形式进行分析和推理
分数形式可以帮助我们进行数据分析和推理。通过运用分数形式进行统计、平均数计算等,可以得出更准确的结论。
12.分数形式在几何问题中的应用
分数形式在几何问题中也有重要作用。例如,计算面积、体积等时,我们需要将分数形式应用于计算过程中。
13.分数形式的误差计算与控制
在实际问题中,我们经常需要进行误差计算与控制。通过运用分数形式进行精确计算,可以有效避免误差累积。
14.分数形式的思维训练与拓展
分数形式的学习还可以培养我们的思维能力和解决问题的能力。通过进行分数形式的思维训练和拓展,我们可以提高自己的数学思维能力。
15.分数形式的实践应用与实验研究
分数形式在实际应用和实验研究中都有重要地位。通过实践和研究,我们可以不断地探索和应用分数形式的新方法和技巧。
掌握打出分数形式的方法是提高学习效果的重要环节。通过理解分数的概念、掌握基本运算规则、运用各种转换和应用方法,我们可以更好地运用分数形式进行学习和解决实际问题。希望本文介绍的方法和技巧能够帮助大家提高学术成绩,更好地应对学习中的各种挑战。


